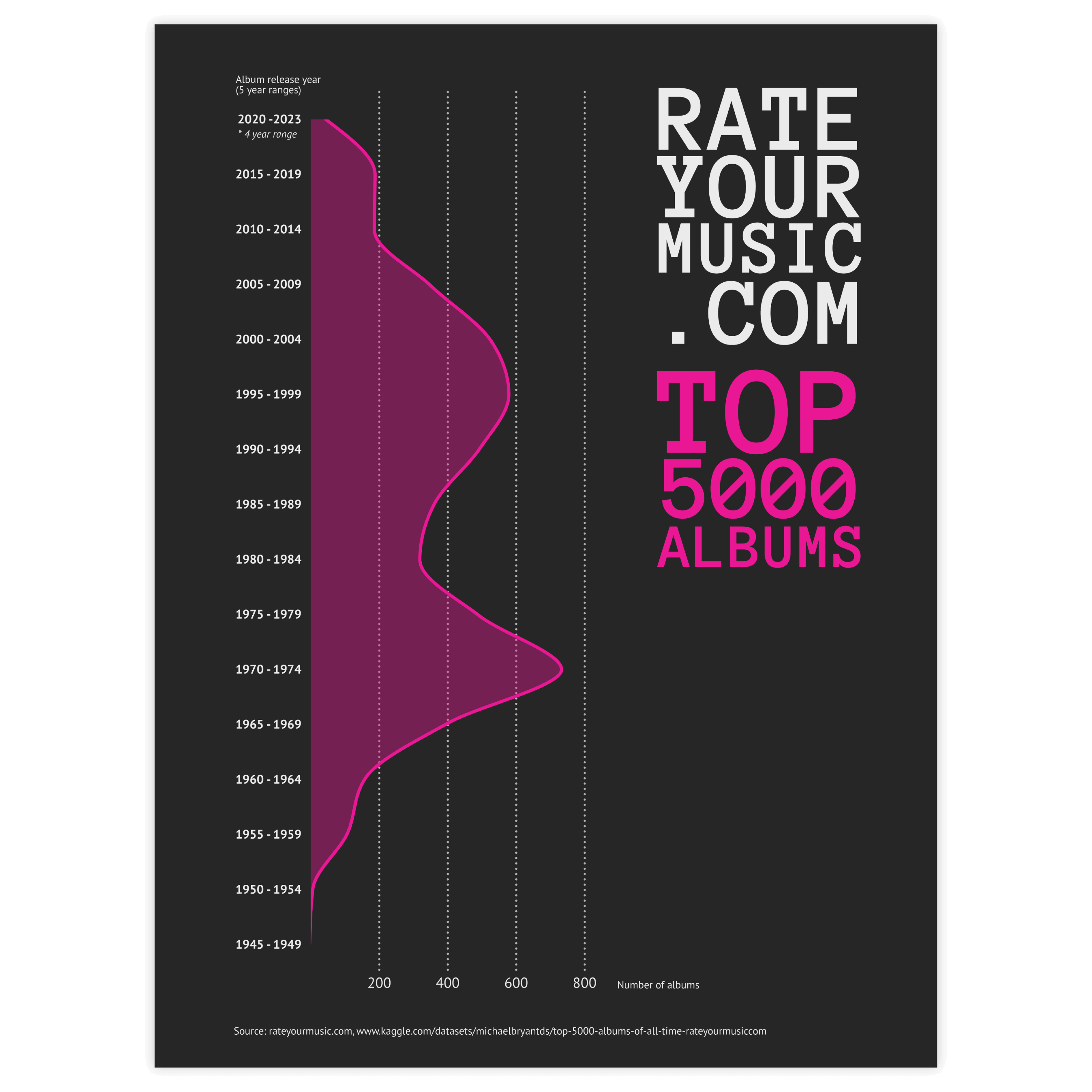
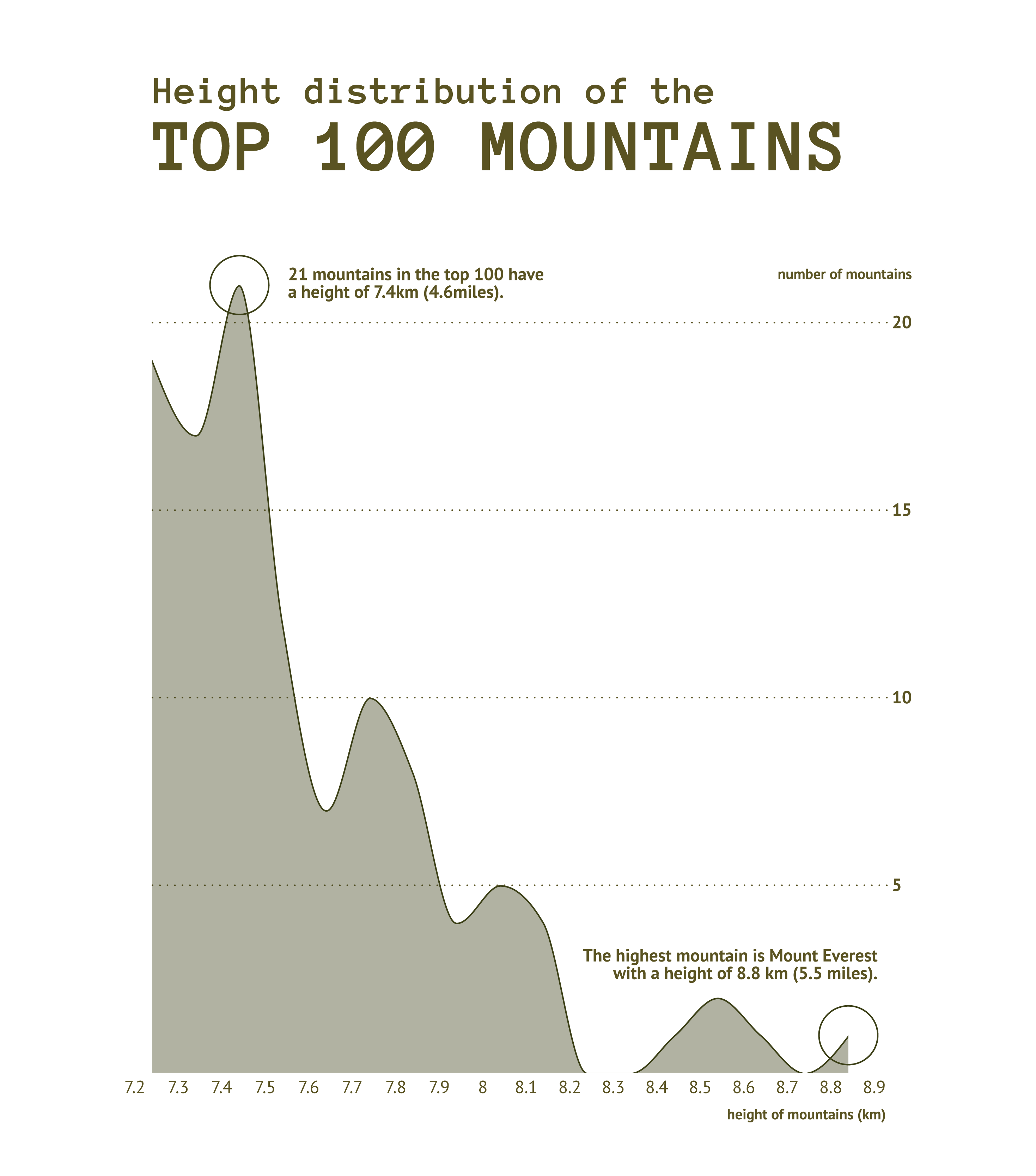
Density Plot
DATYLON > CHART LIBRARY > DENSITY PLOT
What is a density plot?
Density plot examples & inspiration
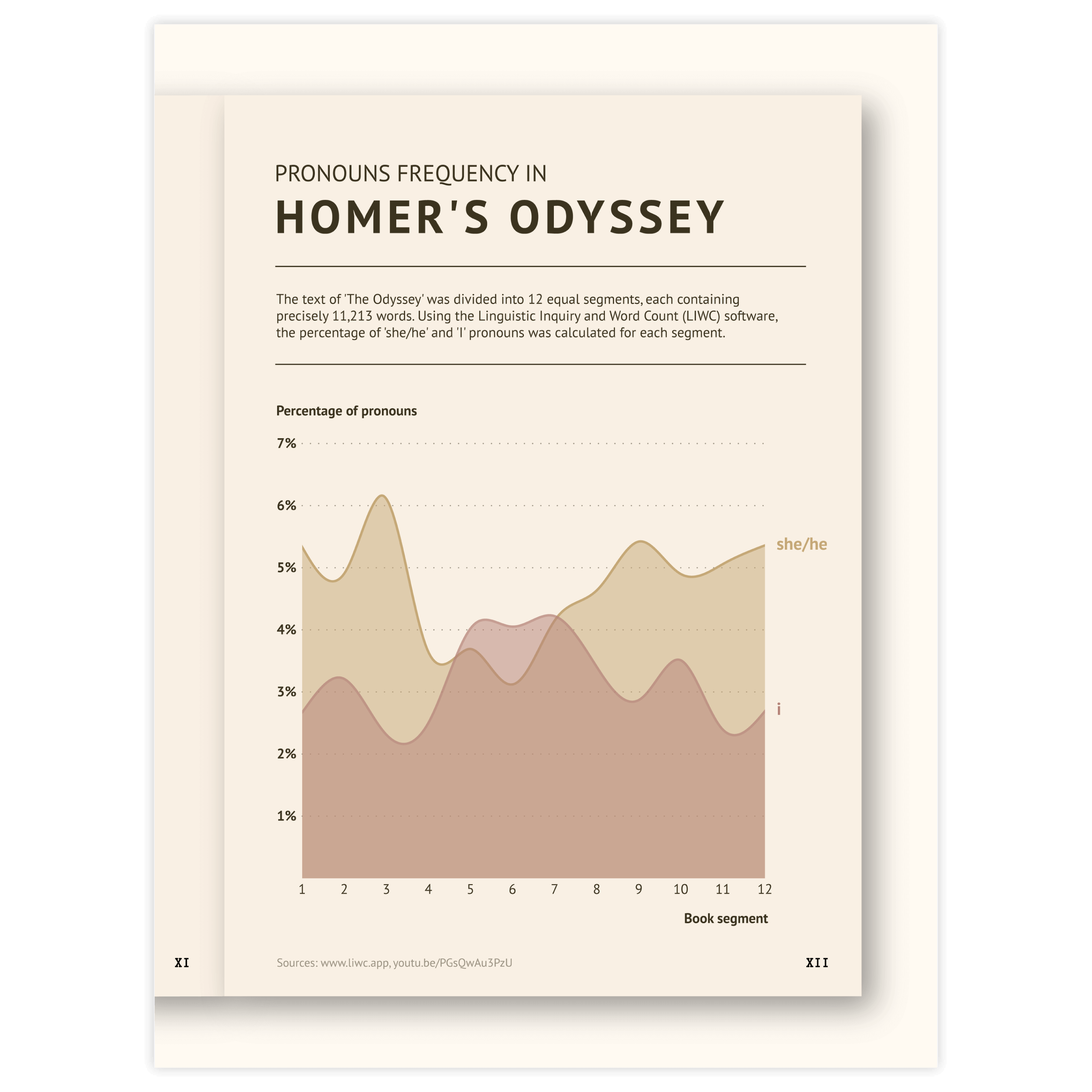
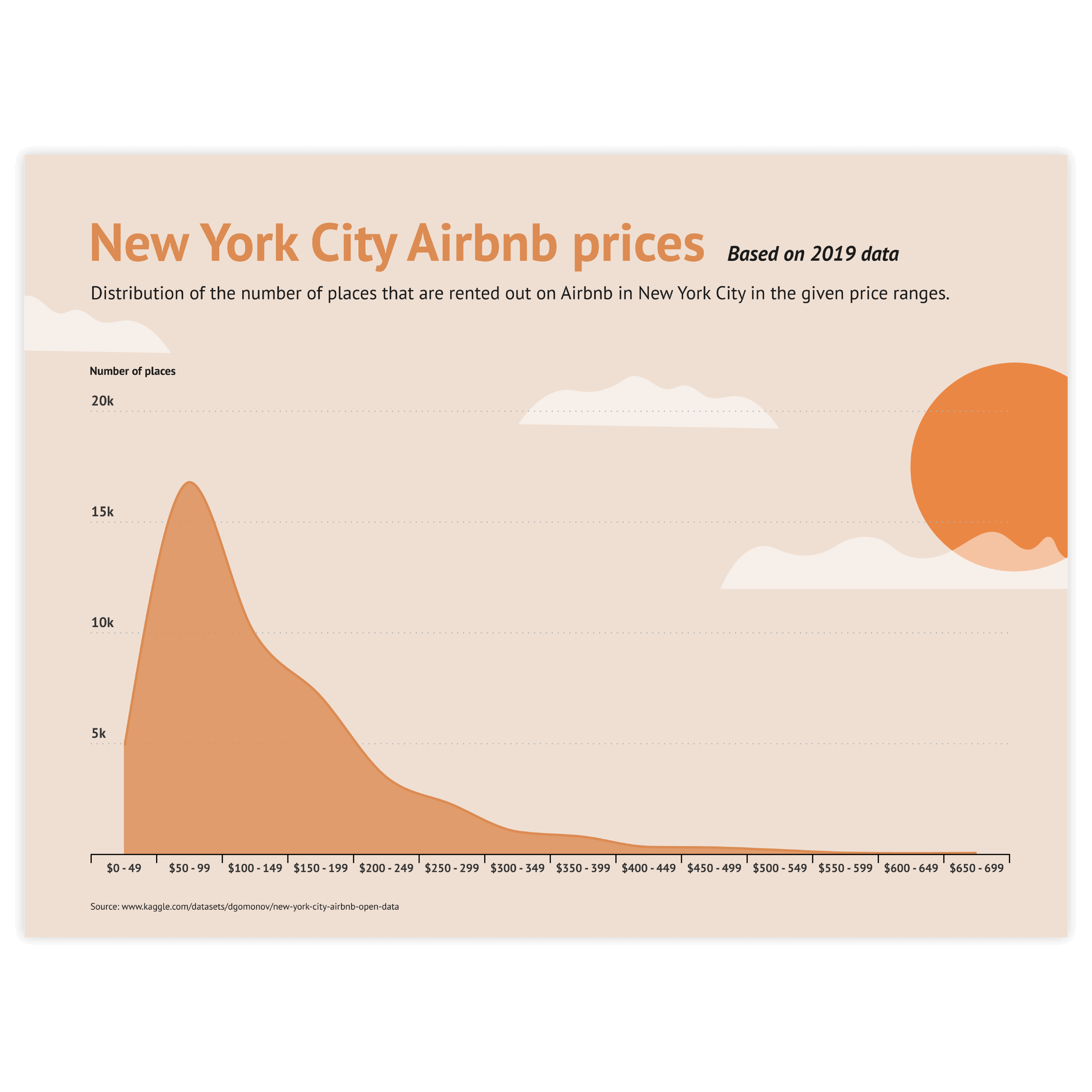
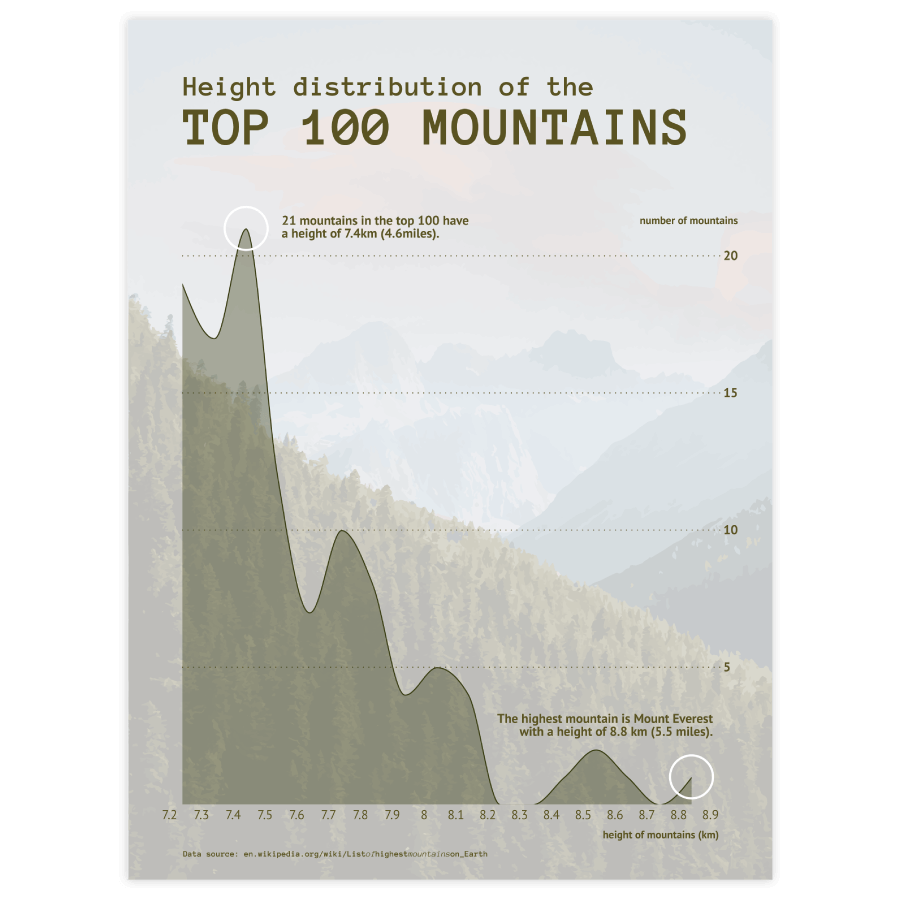
Scroll and click on the images below to find inspiration samples of density plots. With your Datylon account, you can use these designs, customize them and update them with new data. Or start designing your very own density plot!
Variations of a density plot
The charts below are variations of a density plot. To learn how to make them with Datylon, check out the area chart user documentation in the Datylon Help Center.
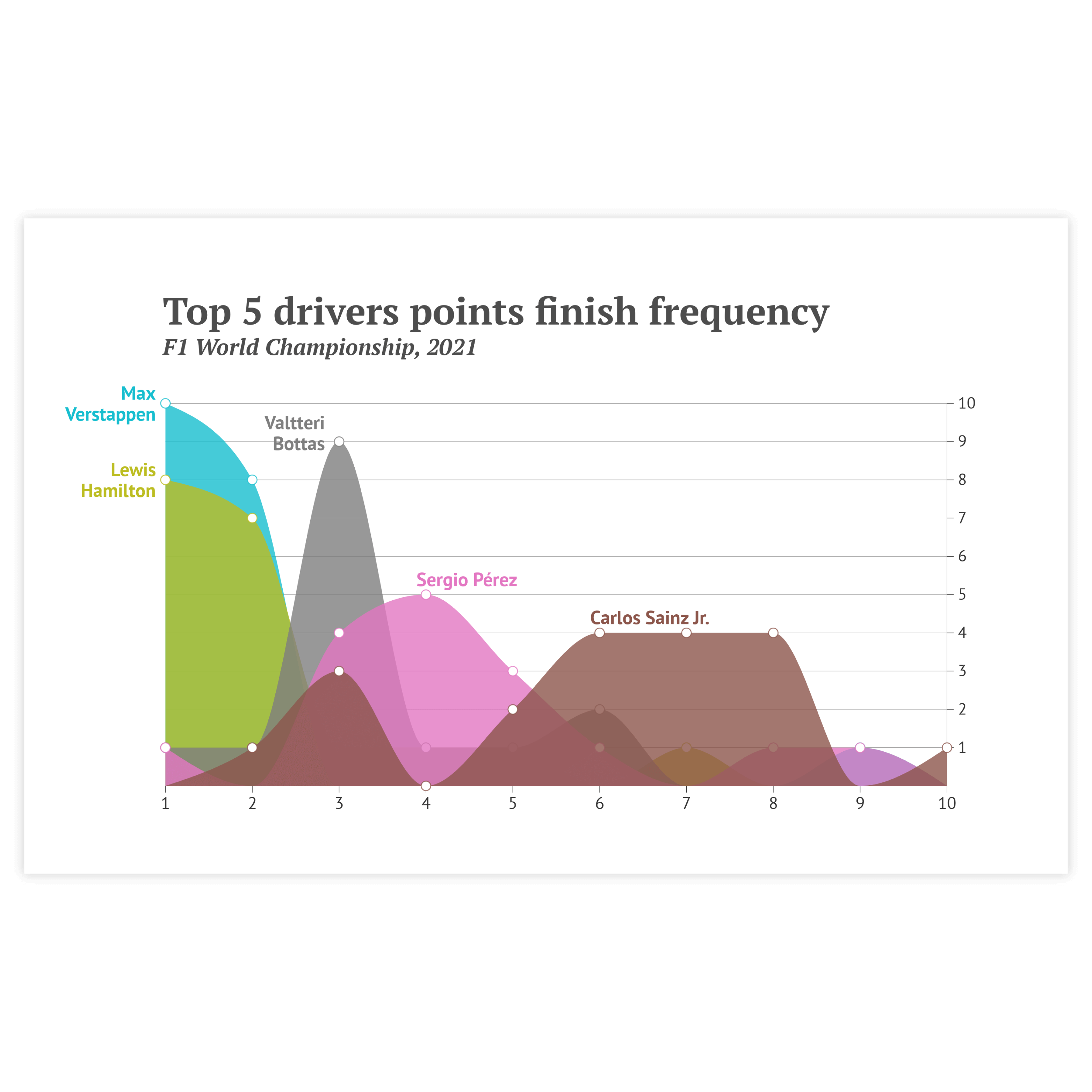
Ridgeline plot
A ridgeline plot (also known as a joy plot) shows the distribution of a numeric value for several groups of a category. It is done by illustrating partially overlapping line charts or area charts. This way, the chart resembles a mountain range. The alternative name for a ridgeline plot is a joy plot because this very example above appeared on the first album cover of the British band Joy Division (‘Unknown Pleasures’ from 1979).
Horizon chart
This is essentially a chopped-up ridgeline plot. If overlappings used in a ridgeline are either confusing or take too much space, every chart is sliced into bands of the same height. Then they are colored: the higher the band value the stronger color's intensity. Then they are placed on top of each other – low-value bands – underneath, high-value – above. If placed this way, all the values are visible and take significantly less space.
Streamgraph
While the density plot is placed strictly above the X-axis line, the streamgraph expands symmetrically on both sides of the axis. While it might require a different way of reading, excluding the possibility to see every value precisely, it also allows us to see the form of distribution. Usually, a streamgraph contains several series/categories, but a single-category streamgraph could also effectively be used instead of a density plot.
Alternatives to a density plot
Substitute your density plot with the charts below when you want an alternative representation of the data distribution.
Violin plot
A violin plot can be perceived as a combination of a density plot (or streamgraph) and a box-plot, showing not only the form of distribution but also the key points of the data: the interquartile range and the median.
Pro tips for designing a density plot
Learn how to improve the readability and visual appeal of your density plot.
Band sizing
The size of the band works basically the same as bins for histograms: depending on the size of the band the form of the density plot can be changed significantly, so It’s better to follow your data’s logic.
For bins, there’s also a popular way of choosing their size called Sturge’s rule. It can be also used for density plots. The formula is the following:
K=1+3.322 log(n),
where:
K is the number of bands
n is the number of observations in a dataset.
Overlapping
For multiple distributions stacking is not a good solution considering that the form of the 2nd and subsequent distributions can’t be determined. In case of numerous distributions, the best option is to use overlapping areas with reduced opacity. In this case, multiple distributions can be seen at the same time.
Number of shown distributions
While using overlapping areas for visualizing multiple distributions can be a good solution it’s better not to exceed the number of shown distributions above three as it can introduce visual clutter.
Mirroring
As an alternative to overlapping areas for two distributions a mirroring over the X-axis can be a solution. While it can lack a relative comparison of distributions this view is definitely visually cleaner.